KMP算法的概要理解

KMP算法，是一种字符串匹配算法，刷题可见Leetcode 28，其中“KMP”由三位提出者名字的首字母组成，没什么特殊含义。该算法的核心，是用空间换时间，通过使用部分匹配表来加速字符串匹配的过程。

首先考虑字符串匹配这个问题。如何判断一个字符串是否为另一个更长字符串的子串呢？最直接的想法就是遍历长串M，每次取出一个长度和目标串N相同的subString进行对比，遍历过程中出现了则是有，遍历到最后都没出现则是无。

这个过程，最坏情况下，对长串M的每一个位置都要进行目标串长度N次的对比，时间复杂度粗略记为O(M * N)。这种解法应该是大部分人第一时间直接想到的解法，但正如《剑指offer》中所言，第一时间想到的解法往往时空效率不够好，对面试来说大概率也不是面试官所期待的。那如何加速字符串匹配过程呢？

废话不多说，下面进入正题

KMP算法中，一个核心概念是Partial Match Table（PMT），参考前人翻译成“部分匹配表”，用一句话来解释其含义，就是用一张表记录了待匹配字符串每个位置的子串，最大的前缀/后缀公共长度。举个例子，待匹配字符串为“abababc”时，如何生成它的部分匹配表？

当走到0时，子串为a，此时认为不存在前后缀，值为0；
当走到1时，子串为ab，此时前缀为{a}，后缀为{b}，值为0；
当走到2时，子串为aba，此时前缀为{a,ab}，后缀为{ba,a}，最长公共部分为a，值为1；
当走到3时，子串为abab，此时前缀为{a,ab,aba}，后缀为{bab,ab,b}，最长公共部分为ab，值为2；
……

这样遍历完整个待匹配串后，就可以对每个位置记录一个部分匹配值，生成一张部分匹配表，对于上面的例子来说，这张表如下图所示，绿色部分为最终结果，灰色部分为计算过程。

有了这张待匹配串的部分匹配表之后，在字符串匹配过程中如何使用这张表呢？仍然以“abababc”为例子，尝试去匹配找其中是否有目标串“ababc”。

上下两个指针从0开始匹配，走到4时发现不对劲，c和a配不上，这时候前面已经走过的abab和abab是匹配的。我们观察已经匹配成功的最后一个位置，也就是位置3上对应的b，它对应的部分匹配值为2，这个2说明的是以该字符结尾的子串，最大公共前缀/后缀长度为2。既然前面已经走过的部分都是匹配的，那么就可以利用这个公共部分，将目标串从开头移动到后面公共的位置，这样就进行了一步加速。
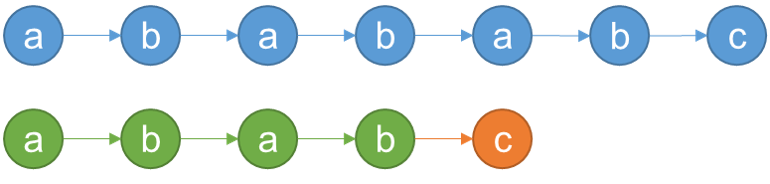
待匹配串的指针位置停留在刚才不对劲的地方，也就是指向a不变，目标串的指针位置向前走，指向的位置是刚才观察的最后一处匹配成功的字符所对应的部分匹配值的位置2。为什么要指向2？因为首尾最大公共前缀/后缀为2，指向2实际上是跳过了这2个公共的字符，指向了从头算起的第3个字符，也就是下图中的橘色a，部分匹配表就是这样被使用的。
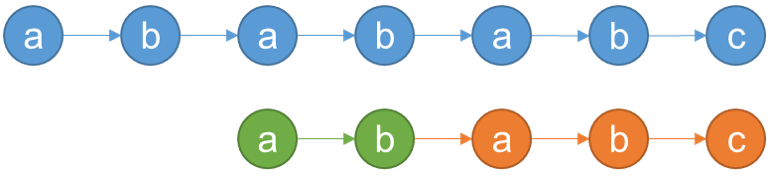
之后，两个指针向后走，最后发现匹配成功！done

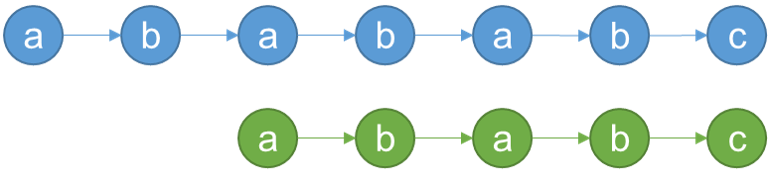
该算法的核心部分就是理解部分匹配表的含义，以及如何在匹配过程中使用部分匹配表。在整个过程中，指向待匹配字符串的指针是不用回退的，也就是人们在讨论中常说的“主串不回溯”。只有指向目标串的指针有可能回退，而且每次回退不是盲目的从0开始，而是借助部分匹配表跳到一个最省力的位置，这步操作省力就省在跳过了最长的公共部分。需要注意的是，当发生不匹配时，要观察的位置是当前不匹配位置的前一个位置，也就是已匹配位置的最后一个字符处的部分匹配值。

如果您仔细看到这里，大概已经了解KMP方法思想中的精髓了，但是如何编写KMP算法，那就是完全不同的另一件事了。整个算法不过几十行，但是要理解的话，我不得不加上了几十行的注释。就附在下面，供有缘人阅读，阅读代码可以知道复杂度为O(M+N)，从乘法变成加法，真的佩服。

在实现过程中还有一些点需要注意。首先使用的表并不是PMT表，而是PMT表向右移动了一位的NEXT表，原因很简单，在匹配过程中，只有当后一位匹配不上时，才会用到前一位的pmt值，这样最后一位的pmt值不就浪费了吗？根本不会用到所以没必要计算了。其次，NEXT中0处的初值设为-1，并不是随随便便设置的，设置成-1，可以在回退到0时方便两个指针同时向后走一位。

import java.util.*;

public class Main {
    public static void main(String[] args) {
        int r = strStr("ababababc", "abababc");
        System.out.println(r);
    }
    public static int strStr(String haystack, String needle) {
        // kmp算法
        // 核心思想：使用部分匹配表pmt来加速匹配过程
        // 这里得到的实际上不是pmt，而是pmt的向右移了一位的next
        int[] pmt = getPmt(needle);
        int i = 0;
        int j = 0;
        // 当i=长度或j=长度时，说明 匹配完成 或者 匹配失败
        while(i<haystack.length() && j<needle.length() ){
            // j=-1说明调用了 j = pmt[0]
            // 其实就是说明在j=0的时候，当前字符不匹配，则j就转到了-1
            // 这时候，i++，j++，就是i向下走一位，j重新回到0的位置

            // 或者当前两个位置的字符一致，就继续向后匹配
            if(j == -1 || haystack.charAt(i) == needle.charAt(j)){
                // 如果匹配结束，i为匹配子串位置的下一个字符，j为匹配的pattern的长度
                // 所以如果j到了pattern的长度，说明匹配成功，并且结果处只需要用i-j即可得到匹配的起点
                i++;
                j++;
            }else{
                // 当前两个位置的字符不一致
                // 说明要移动pattern，这里用next数组进行加速
                // 根据前一个位置的最长公共前缀和后缀，可以确定pattern指针j应该指到哪
                // 又因为next实际是pmt右移一位，所以直接就是j=pmt[j]而不需要j=pmt[j-1]
                j = pmt[j];
            }
        }
        if(j == needle.length()){
            return i-j;
        }else{
            return -1;
        }
    }

    // 生成 向右移一位 的部分匹配表
    public static int[] getPmt(String needle){
        // 第一个位置设为-1
        // 实际上这里得到的是next，而不是pmt，前者是后者右移了一个单位，方便使用
        // 当后一位不匹配时，才会用到前一个位置的pmt值，所以说pattern的最后一个位置的pmt值是多余的
        int[] next = new int[needle.length()];
        next[0] = -1;

        int i = 0;
        int j = -1;
        while(i<needle.length()-1){
            //j为-1，说明是最开始，第一个字符的公共前后缀为0没错
            //或者两个字符一致，说明当前两个字符匹配，都可以向后走一步
            //下一个位置的next指向j+1，j是字符一致的位置，j+1是下次开始考虑的位置
            if(j == -1 || needle.charAt(i) == needle.charAt(j)){
                next[i+1] = j+1;
                i ++;
                j ++;
            }
            //不是最开始，并且两个字符不匹配
            //则需要调整j到左侧最近的位置
            else{
                j = next[j];
            }
        }
        return next;
    }
}